1. 인접 행렬 vs 인접 리스트
2. 순회

그래프는 연결되어 있는 객체간의 관계를 표현할 수 있는 자료 구조이다.
수학자 오일러에 의해 처음 창안되어 그래프 이론은 컴퓨터 학문 분야의 활발한 연구 주제이다.
그래프에 관한 아주 간단한 설명은 이전 게시글에 있다.
2. 자료구조 (2) - 트리, 그래프
트리 트리 = 노드(node)로 이루어진 자료 구조. 하나의 루트 노드가 존재하고, 이로부터 0개 이상의 자식 노드들이 존재합니다. 이 노드들이 서브트리(subtree)를 구성합니다. 루트와 서브 트리, 각�
howtolivelikehuman.tistory.com
1. 인접 행렬 vs 인접 리스트
그래프를 표현하는 방법은 두가지가 있다. 인접 행렬과 리스트

인접행렬 M의 각 원소를 아래와 같은 규칙에 따라 그래프를 메모리에 표현할 수 있다.
if(간선 x,y가 그래프에 존재) M[x][y] = 1;
otherwise M[x][y] = 0만약 Undirected(무방향) 그래프에서 이런 식으로 표현한다면, 배열의 절반 삼각형만 저장하여 메모리를 절약할 수 있다.
Directed(방향) 그래프에서 역시 비슷하게 표현할 수 있다.
이러한 표현 방법은 모든 정점의 제곱만큼 무조건 만들어야 하기 때문에 그래프에 간선이 많이 존재하는 밀집 그래프(dense graph)를 표현하는 경우에 적합하다.
반면 희소 그래프(sparse graph)의 경우에는 메모리의 낭비가 크다.
행렬이기 때문에 두 정점을 연결하는 간선의 존재 여부를 O(1) 시간 안에 즉시 알 수 있다. M[x] [y]만 조사한다면 바로 알 수 있기 때문이다. 또한 정점의 차수 (몇 개가 연결되어 있는지)는 그 정점이 해당하는 행을 다조사하면 O(n)의 연산으로 알 수 있다.
정점 i에 관한 차수는 따라서 ∑n−10M[i][k]로 알 수 있고, 모든 그래프의 차수는 O(n2)의 시간이 요구된다.
#define MAX_VERTICES 30
typedef struct GraphType{
int n;
int adj_mat [MAX_VERTICES][MAX_VERTICES]
}GraphType;
void graph_init(GraphType *g){
int r,c;
g->n =0;
for(r=0; r<MAX_VERTICES; r++)
for(c=0; c<MAX_VERTICES; c++)
g->adj_mat[r][c]=0;
}
void insert_vertex(GraphType *g, int v){
if(((g->n)+1) > MAX_VERTICES){
fprintf(stderr, "그래프 : 정점 개수 초과");
return
}
g->n++;
}
void graph_init(GraphType *g, int start, int end){
if(start >= g->n || end >= g->n){
fprintf(stderr,"그래프 : 정점 번호 오류");
return
}
g->adj_mat[start][end] = 1;
g->adj_mat[end][start] = 1;
}c++인접 리스트는 각각의 정점에 인접한 정점들을 연결리스트로 표시한 것이다. 리스트에 노드들은 정점을 포함하게 된다. 각 연결 리스트는 헤드포인터를 가지고 있고, 이 헤드 포인터들은 배열로 구성되어 있다. 정점의 번호만 알면 배열의 인덱스처럼 접근에 정점의 연결리스트에 접근하는 것이다.
무방향 그래프에서 정점위 수가 n개이고, 간선의 수가 e개인 경우 n개의 연결 리스트가 필요하고 n개의 헤드 포인터가 필요하다. 또 노드는 2e개 가 필요하다. i에서 j로 가는 정점과 j에서 i로 가는 정점이 모두 성립해 중복해서 노드가 생기는 것이다.
인접 행렬로 표현했을 때는 메모리의 크기가 전체 정점의 개수에 좌우되었다면, 인접 리스트는 간선의 개수에 좌우된다. 따라서 간선이 적은 희소 그래프의 표현에 적합하다.
#define MAX_VERTICES 30
typedef struct GraphNode{
int vertex;
struct GraphNode*link;
}GraphNode;
typedef struct GraphType{
int n;
GraphNode *adj_list[MAX_VERTICES];
}GraphType;
void graph_init(GraphType *g){
int v;
g->n = 0;
for(v =0; v<MAX_VERTICES){
G->adj_list[v] = NULL;
}
}
void insert_vertex(GraphType *g){
if(((g->n)+1) > MAX_VERTICES){
fprintf(stderr, "그래프 : 정점 개수 초과");
return
}
g->n++;
}
void insert_edge(GraphType *g, int u, int v){
GraphNode *node;
if(u >= g->n || v>= g->n){
fprintf(stderr,"그래프 : 정점 번호 오류");
return
}
node = (GraphNode *)malloc (sizeof(GraphNode));
node -> vertex = v;
node -> link = g-> adj_list[u];
g-> adj_list[u] = node;
}c++
2. 순회
하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하는 것을 그래프 순회(Graph tra) 또는 탐색이라고 한다.
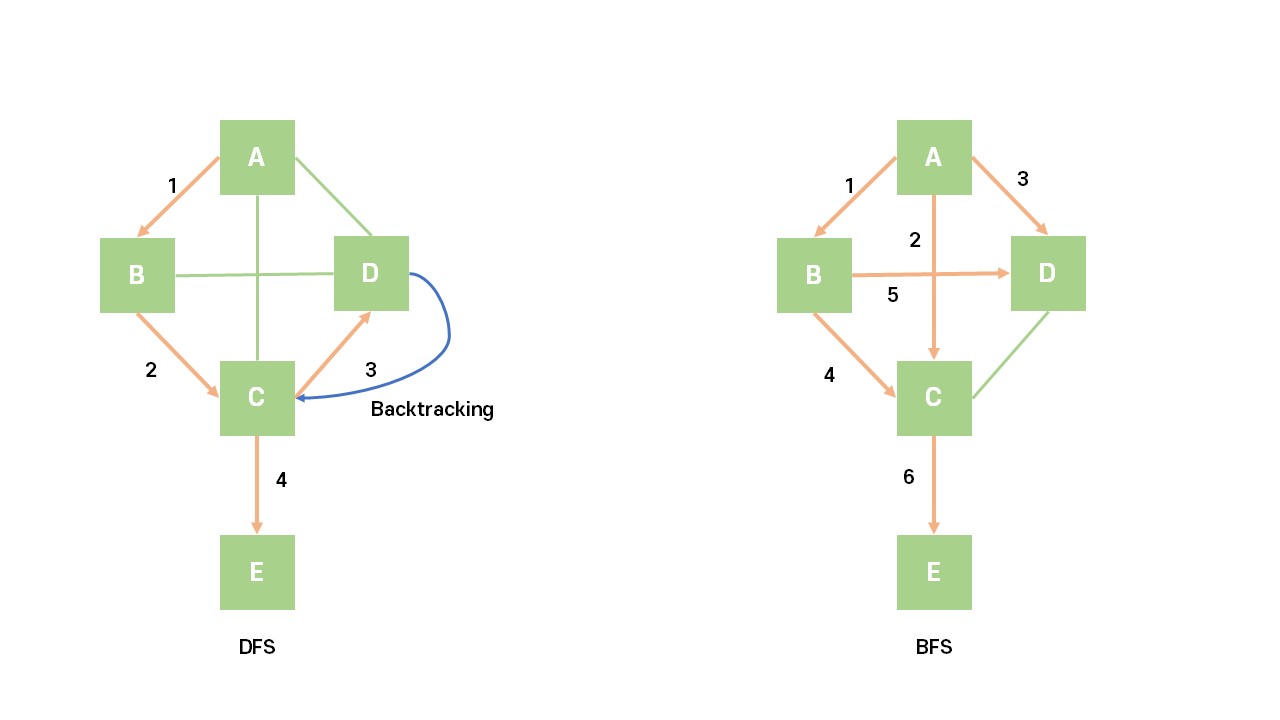
BFS (Breadth-First Search)
너비 우선 탐색은 루트 노드로 부터 시작해서 인접한 노드들을 먼저 탐색하는 것이다.
- 시작 점으로부터 가까운 점을 먼저 방문하고 멀리 있는 애들을 나중에 방문하는 순회방법이다.
- 깊게가 아니라 넓게 <-> DFS
- 두 노드 사이의 최단 경로 or 임의의 경로를 찾고 싶을때 이 방법을 선택.
- 재귀적으로 동작하지 않는다 (계속 인접 노드들을 향해 나아가기만 함)
→ 어떤 노드를 탐색했는지의 여부를 반드시 검사해야 한다. (안그럼 무한루프) - 방문한 노드들을 차례로 저장하고 꺼내기 위해 큐(QUEUE) 사용. 즉 선입선출(FIFO) 원칙으로 탐색한다.
- 그래프가 인접 리스트로 표현된 경우 O(N), 인접 행렬로 표현되었을 경우 O(N2)의 시간복잡도를 가진다.
BFS는 시작점(V)를 큐에 넣고, point로 삼은 다음에 0부터 for문을 돌아서 방문할 수 있는 노드들을 쭉 방문한다.
이후 방문한 노드들을 다시 하나씩 뱉으며 이 지점에서 또 방문할 수 있는 노드들을 쭉 방문한다.
#define _CRT_SECURE_NO_WARNINGS
#define MAXSIZE 100000
#include <stdio.h>
#include <stdbool.h>
//queue 구현용 전역변수들
int front = -1, rear = -1;
int queue[MAXSIZE];
int** root;
int N, M, V;
//QUEUE 구현
int putqueue(int val) {
if ((rear + 1) % MAXSIZE == front) { // 큐가 꽉 찼는지 확인
return -1;
}
queue[rear] = val; // rear가 큐의 끝 다음의 빈공간이므로 바로 저장
rear = ++rear % MAXSIZE; // rear를 다음 빈공간으로 변경
return val;
}
int getqueue(void) {
int i;
if (front == rear) { // 큐가 비어 있는지 확인
return (-1);
}
i = queue[front]; // front의 값을 가져옴
front = ++front % MAXSIZE; // front를 다음 데이터 요소로
return i;
}
void init_queue(void) {
front = rear = 0;
}
void clear_queue(void) {
front = rear;
}
//BFS 구현
void BFSsearch() {
int point;
int pathcheck = 0;
int *path = (int*)calloc(N, sizeof(int));
for (int i = 0; i < N; i++) {
path[i] = 0;
}
putqueue(V-1);
path[V-1] = 1;
printf("%d ", V);
//queue 구현시에 rear = front 면 queue가 비어있는걸로 함.
while (rear != front) {
point = getqueue();
for (int i = 0; i < N; i++) {
if ((path[i] != 1) && (root[point][i] == 1)) {
putqueue(i);
printf("%d ", i+1);
path[i] = 1;
}
}
}
free(path);
return;
}
int main(void) {
int i, y,x;
scanf("%d %d %d", &N,&M,&V);
getchar(); //\n 받기
//2차원 배열들 동적할당
root = (int**)calloc(N,sizeof(int*));
for (i = 0; i < N; i++) {
root[i] = (int*)calloc(N, sizeof(int));
}
for (i = 0; i < M; i++) {
scanf("%d %d",&y,&x);
root[y-1][x-1] = 1;
root[x-1][y-1] = 1;
}
DFSsearch();
return 0;
}c++DFS(DFS, Depth-First Search)
깊이 우선 탐색은 루트 노드로 부터 시작해서, 다음 분기로 넘어가기 전에 해당 분기를 모두 탐색하는 것이다.
- 한 방향으로 계속 가다가 더 갈수 없게 되면 다시 가까운 갈림길로 돌아와서 탐색하는 방법이다.
- 넓게가 아니라 깊게 <-> BFS
- 모든 노드를 방문하고 싶을때 이 방법을 선택.
- 재귀적으로 동작한다.(자기 자신을 계속 호출)
-> 전위 순회같은 트리 순회들은 모두 DFS의 한 종류 - 구현 방법은 2가지로 순환 호출을 사용하거나, 스택을 사용하여 정점을 스택에 저장했다가 꺼내서 작업한다.
- 그래프가 인접 리스트로 표현된 경우 O(N), 인접 행렬로 표현되었을 경우 O(N2)의 시간복잡도를 가진다.
DFS는 queue를 구현하여 탐색을 하였다.
DFS는 시작점(V)를 스택에 넣고, point로 삼은다음에 역순으로 for문을 돌아서 해당 지점에서 방문할 수 있는 노드들을 (방문 아직 안한) 큐에 넣는다.
이후 하나씩 pop하며 만약 pop한 노드가 아직 방문을 안했다면 방문한다(출력) 그리고 방문했다고 표시. 이를 스택이 비워질때까지 반복한다.
#define _CRT_SECURE_NO_WARNINGS
#define MAXSIZE 100000
#include <stdio.h>
#include <stdbool.h>
//stack 구현용 전역변수들
int stack[MAXSIZE];
int top = -1;
int** root;
int N, M, V;
//STACK 구현
int IsEmpty() {
if (top < 0)
return true;
else
return false;
}
int isFull() {
if (top >= MAXSIZE-1)
return true;
else
return false;
}
void push(int val) {
if (isFull() == true) {
return;
}
else {
stack[++top] = val;
}
}
int pop() {
if (IsEmpty() == true) {
return;
}
else {
return stack[top--];
}
}
void DFSsearch() {
int point;
int* path = (int*)calloc(N, sizeof(int));
for (int i = 0; i < N; i++) {
path[i] = 0;
}
push(V - 1);
path[V - 1] = 1;
//시작점
point = V - 1;
printf("%d ", point+1);
while (!IsEmpty()) {
for (int i = N-1; i >= 0; i--) {
if ((path[i] != 1) && (root[point][i] == 1)) {
push(i);
}
}
point = pop();
if (path[point] != 1) {
printf("%d ", point+1);
path[point] = 1;
}
}
free(path);
return;
}
int main(void) {
int i, y,x;
scanf("%d %d %d", &N,&M,&V);
getchar(); //\n 받기
//2차원 배열들 동적할당
root = (int**)calloc(N,sizeof(int*));
for (i = 0; i < N; i++) {
root[i] = (int*)calloc(N, sizeof(int));
}
for (i = 0; i < M; i++) {
scanf("%d %d",&y,&x);
root[y-1][x-1] = 1;
root[x-1][y-1] = 1;
}
BFSsearch();
return 0;
}c++
'알고리즘 > 스터디' 카테고리의 다른 글
| 13. 카라추바 알고리즘 (큰 수의 곱) [JAVA] (0) | 2020.12.26 |
|---|---|
| 12. 그래프 (2) (최단경로, 프림, 크루스칼) (0) | 2020.09.14 |
| 10. 순열과 조합 [JAVA] (0) | 2020.09.02 |
| 9. 최대, 최소 찾기 (순차, 토너먼트, 선택 알고리즘) (0) | 2020.09.01 |
| 8. 탐색 - 선형 탐색, 이진 탐색, 이진 탐색 트리, 해시 탐색 (0) | 2020.08.25 |

Comment