1. 비트 조작

1. 비트 조작
비트(bit)는 Binary Digit를 줄인 말로 데이터를 나타내는 최소 단위이다. 0과 1 두 값 중 하나를 가질 수 있다.
8bit가 모여서 1Byte가 되며 이후 단위들은 아래와 같다.
| 접두어(SI) | 이름 | 계산법 | 접두어(IEC) | 이름 | 계산법 |
|---|---|---|---|---|---|
| 킬로(103) | 1킬로바이트(kilobyte)/kB | 1000B=1kB | 키비(210) | 1키비바이트(kibibyte)/KiB | 1024B=1KiB |
| 메가(106) | 1메가바이트(megabyte)/MB | 1000KB=1MB | 메비(220) | 1메비바이트(mebibyte)/MiB | 1024KiB=1MiB |
| 기가(109) | 1기가바이트(gigabyte)/GB | 1000MB=1GB | 기비(230) | 1기비바이트(gibibyte)/GiB | 1024MiB=1GiB |
| 테라(1012) | 1테라바이트(terabyte)/TB | 1000GB=1TB | 테비(240) | 1테비바이트(tebibyte)/TiB | 1024GiB=1TiB |
| 페타(1015) | 1페타바이트(petabyte)/PB | 1000TB=1PB | 페비(250) | 1페비바이트(pebibyte)/PiB | 1024TiB=1PiB |
| 엑사(1018) | 1엑사바이트(exabyte)/EB | 1000PB=1EB | 엑사(260) | 1엑스비바이트(exbibyte)/EiB | 1024PiB=1EiB |
| 제타(1021) | 1제타바이트(zettabyte)/ZB | 1000EB=1ZB | 제비(270) | 1제비바이트(zebibyte)/ZiB | 1024EiB=1ZiB |
| 요타(1024) | 1요타바이트(yottabyte)/YB | 1000ZB=1YB | 요비(280) | 1요비바이트(yobibyte)/YiB | 1024ZiB=1YiB |
실제로는 킬로, 메가 기가 등등 모두 210으로 계산한다.
이러한 비트 조작은 비트연산자를 통해 계산할 수 있다.
- NOT(~)
각 자리수의 값을 반대로 바꾸는 연산.
(NOT 1010 = 0101, x = ~x) - OR (|)
두 자릿수 중 하나라도 1이 있으면 1로, 없으면 0으로 하는 연산
1010 OR 0101 = 1111, X = X|Y - AND (&)
두 자릿수 중 하나라도 0이 있으면 0으로, 없으면 1로 하는 연산
1010 AND 0101 = 0000, X = X&Y - XOR (^)
두 자릿수의 값이 다르면 1, 같으면 0으로 하는 연산
1010 XOR 0101 = 1111, X = X^Y; - NOT(~)
각 자리수의 값을 반대로 바꾸는 연산.
(NOT 1010 = 0101, x = ~x)
시프트 연산
시프트 연산은 비트들의 자릿수를 이동시키는 것으로 두 가지 종류가 있다.

산술시프트
">> n " 면 오른쪽으로, "<< n"면 왼쪽으로 비트를 n 칸씩 이동 시키는 것이다.
만약 범위를 초과하게 되면 초과 자릿수는 소멸되고, 빈 자릿수는 0으로 채워진다.
하지만 정수의 부호는 바뀌지 않는다. 만약 오른쪽 시프트일때 ( >> ) 음수면 최상위 비트가 1이고, 이때는 자릿수를 1로 채운다.
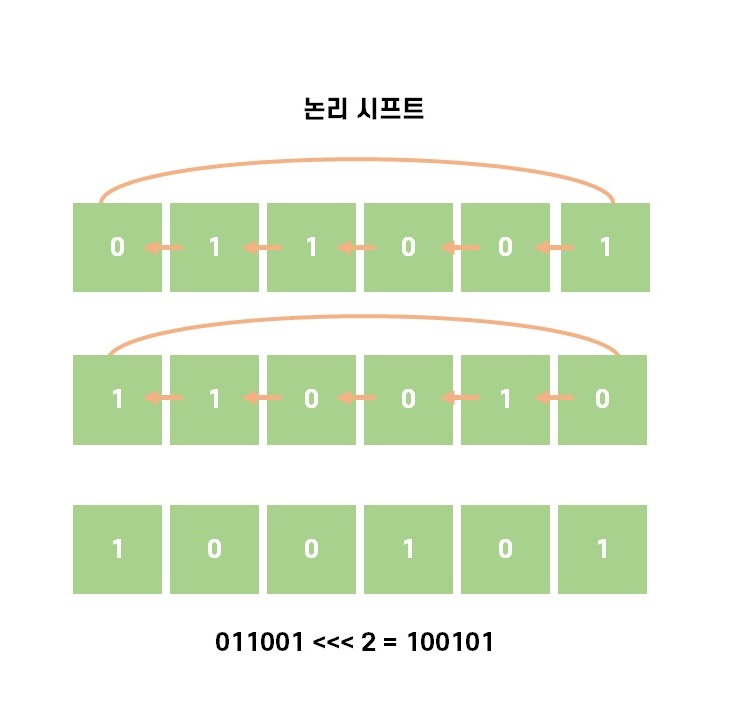
논리 시프트
">>> n" 이면 오른쪽으로 , "<<< n"이면 왼쪽으로 비트를 n칸씩 회전시키는 것이다.
범위를 초과하게 되면 초과 자릿수는 다시 빈 자릿수로 채워진다.
보통 암호 알고리즘에 주로 사용되는데, 직접 구현해야 할 필요가 많다.
#define RotateR(word , bit) (((word) >> (bit)) | ((word) << (32-(bit))))c++">>>" 를 부호 없는 정수 범위에서 산술 시프트와 OR를 사용하여 구현한 모습인데
bit만큼 오른쪽으로 >>한 값과 32-bit만큼 왼쪽으로 << 한 값을 or연산하여 회전 시킨 모습이다.
= 00000000000000000000001111111111 | 01010101010100000000000000000000
= 01010101010100000000001111111111
그렇다면 비트 연산의 특징을 알아보자
- 어느 숫자를 2n만큼 곱하는 것은 n만큼 "<<" 하는 것과 같다.
5*4 = 0101 << 2 = 10100 (20)
반대로 2n만큼 나누는 것은 n만큼 ">>"하는 것과 같다. - 어느 숫자에 어느 숫자건 xor을 두 번 취하면 원래 숫자로 돌아간다.
0101 ^ 1010 = 1111 ^ 1010 = 0101
이러한 특성을 이용하여 대칭 암호 알고리즘에 주로 사용된다. - 1111111.... = ~0이다.
이러면 프로그램이 32bit인지, 64bit인지 신경쓰지 않고도 사용할 수 있다.
~11 = 111111111....00
비트 연산은 컴퓨터가 제일 좋아하는 연산이므로 아주 빠르고 효율이 좋다. 이런 비트를 조작하는 함수들도 존재한다.
GET : 특정 위치의 비트 얻어내기
int getBit(int number, int i){
return number & (1 << i); // number | (0 << i)도 가능
}c++SET : 특정 위치의 비트값 1로 채우기
int setBit(int number, int i){
return number | (1 << i);
}c++CLEAR : 특정 위치의 비트 값 삭제하기 (0으로)
int clearBit(int number, int i){
return (number & ~(1 << i));
}c++CLEAR2 : 특정 위치부터 0까지 모두 삭제하기
int clearBitthroughI(int number, int i){
return (number & (~0 << i+1));
}c++UPDATE : 특정 위치의 비트 값 반전
int updateBit(int number, int i){
return number ^ (1 << i);
}c++
'알고리즘 > 스터디' 카테고리의 다른 글
| 6. 정렬 (1) - 삽입 정렬, 버블 정렬, 퀵 정렬 (0) | 2020.08.12 |
|---|---|
| 5. 재귀 호출 - 완전 탐색, 동적 프로그래밍 (0) | 2020.07.31 |
| 3. 자료구조 (3) - 힙, 구조체 (0) | 2020.07.25 |
| 2. 자료구조 (2) - 트리, 그래프 (0) | 2020.07.25 |
| 1. 자료구조 (1) - 배열, 연결리스트, 스택, 큐 (0) | 2020.07.14 |

Comment