1. 트리
2. 그래프

1. 트리
트리 = 노드(node)로 이루어진 자료 구조.
하나의 루트 노드가 존재하고, 이로부터 0개 이상의 자식 노드들이 존재합니다. 이 노드들이 서브트리(subtree)를 구성합니다.
루트와 서브 트리, 각각 노드들간은 간선(edge)로 연결되어 있습니다.
그래프의 한 종류로써 트리는 asyclic connected(undirected) graph, 사이클이 없는 비방향성 그래프입니다.

- 루트 노드 (Root node) : 부모가 없는 노드 (트리의 처음)
- 잎 노드 (Leaf node) : 자식이 없는 노드 (트리의 마지막들)
- 부모 노드(Parent node) , 자식 노드(Child node)의 관계가 있음
- 노드의 깊이(Depth) : 루트노드(0)으로부터 도달하기 위해 거쳐야 하는 간선의 수 (부모 노드의 깊이 +1)
- 노드의 높이(Height) : 루트 노드로부터 가장 큰 깊이
- 노드의 차수(Degree) : 각 노드가 지닌 가지의 개수(자식의 개수)
이진 트리 = 각 노드들이 최대 두 개의 자식 노드를 가지는 트리 구조입니다. (위 사진과 같은 트리 구조)
이때 트리의 순회는 모든 노드들을 중복 없이 방문하는 방법입니다.
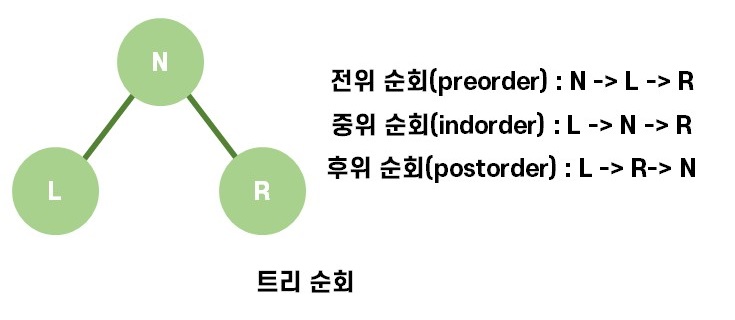
이진 트리의 간단한 공식
- n개의 노드일때 간선 n-1개 간선
- 깊이가 d 일때 노드 최대 2d개
- 높이가 h일때 노드 최대 2h+1−1개
- n개의 노드일때 최소 높이 ⌈lg(n+1)⌉−1
완전 이진 트리 : 트리의 마지막 레벨을 제외하고 노드가 꽉 차 있는 이진 트리.
이진 탐색 트리 : 이진 트리를 기반으로 탐색을 효율적으로 수행하기 위한 트리
모든 노드의 키는 유일하고, 부모를 기준으로 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큰 트리
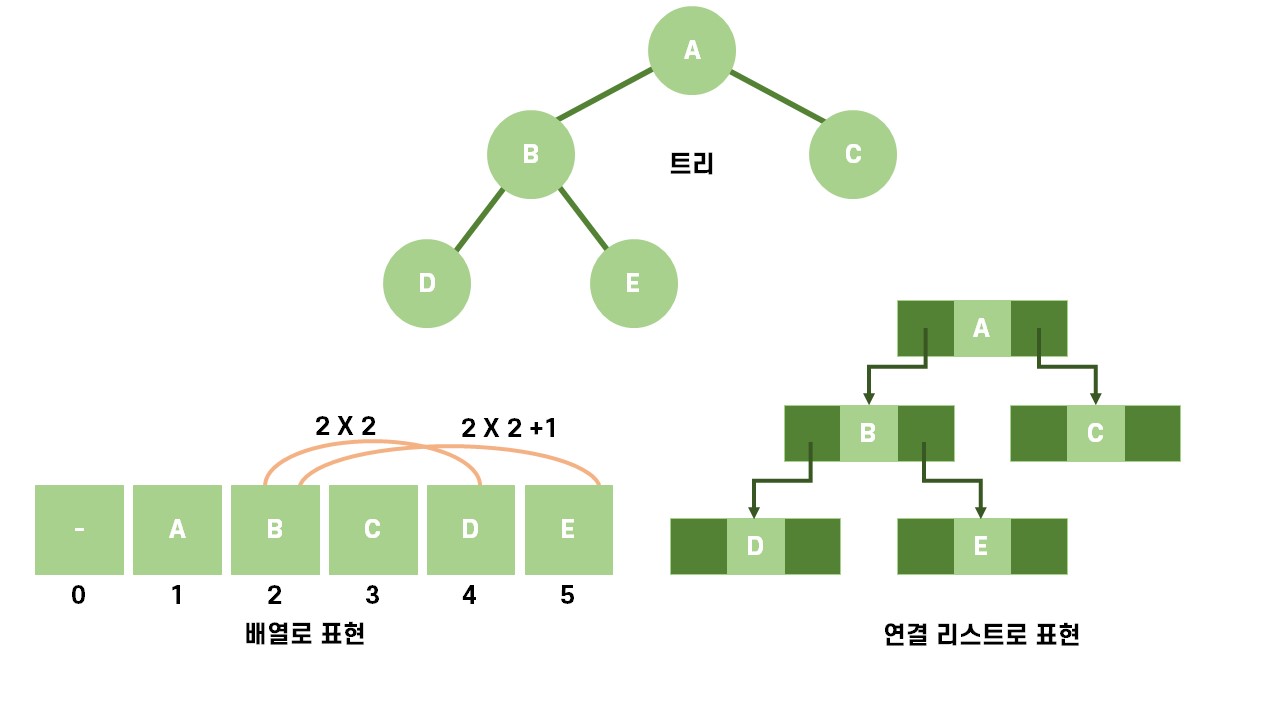
이진 트리는 배열을 사용하여 루트 노드가 1부터 시작한다고 할 때, 그 자식 노드들은 부모 노드 *2, *2+1한 인덱스에 위치하는 방법으로 표현할 수 있음.
연결 리스트로 표현 할 때에는, 양방향 리스트로 왼쪽, 오른쪽 포인터로 자식 노드를 가르키는 방법으로 표현할 수 있음.
2. 그래프
그래프 = 정점(vertices)의 모음과 이 정점을 잇는 간선(edge)의 모음
G=(V,E)로 표현하는데, 이때 부분그래프 G` = (V`,E`) 일때 V`\subseteq V , E`\subseteq E라 할 수 있습니다.
완전 그래프 (Complete Graph) : 모든 정점이 나머지 정점에 간선이 있는 형태.
두 정점간 간선이 연결(incident)된 경우 , 두 정점은 접하고 있다 (adjacent), 인접해 있다(neighbors)라고 합니다.
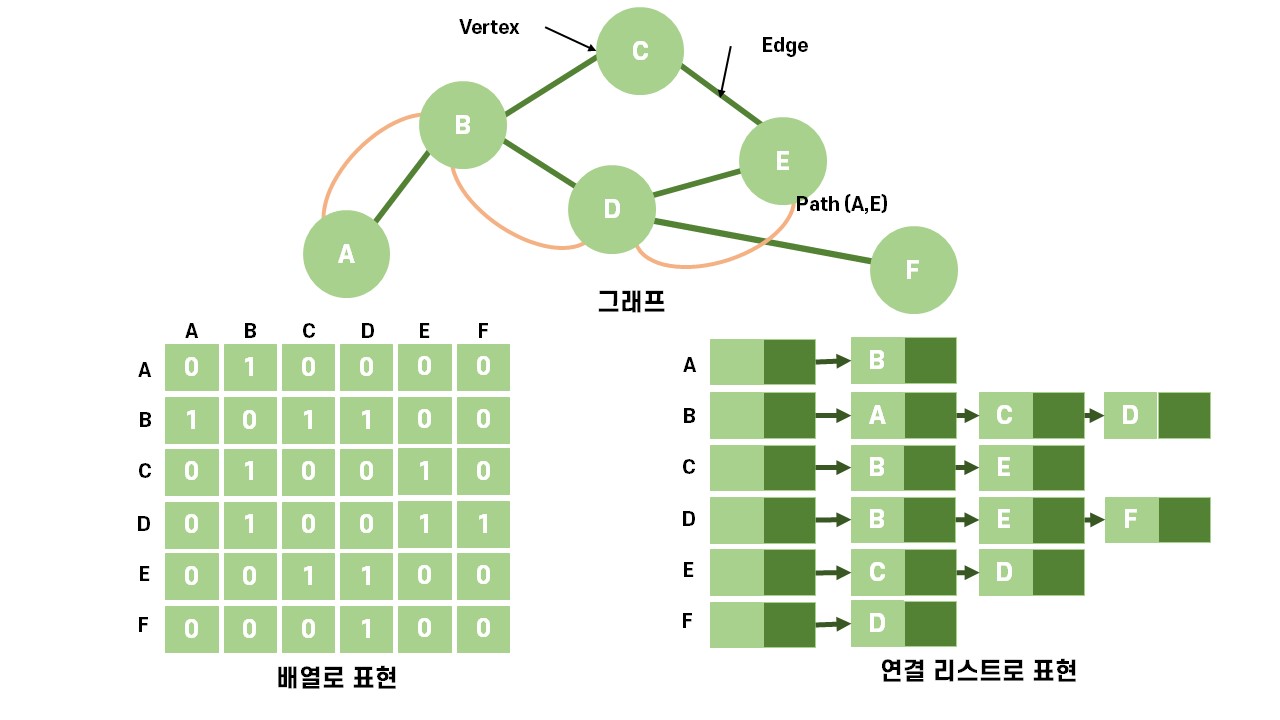
경로(path) = 그래프 G 안의 정점V_1 에서 다른 정점 V_2로 갈때 거쳐야 하는 정점들입니다.
비 방향성 그래프 (Undirected Graph) = 연결(connected)되어 있음 (방향 x)
방향성 그래프(Directed Graph) = 강하게 연결(strongly conneceted)되어 있음. (방향 o)
사이클(Cycle) = 그래프 G에서 자기 자신으로 돌아오는 경로가 있는 경우. / Acyclic = 사이클이 없음2차원 배열로 각 정점 간 간선을 표현할 수 있고, 연결리스트로 표현 시 포인터로 각 정점을 연결하여 구현할 수 있음.
그래프의 간선별로 가중치를 넣은 가중 그래프도 있음. 이때 최단 경로를 찾는 프림, 다익스트라, 크루스칼 알고리즘등이 존재.
'알고리즘 > 스터디' 카테고리의 다른 글
| 6. 정렬 (1) - 삽입 정렬, 버블 정렬, 퀵 정렬 (0) | 2020.08.12 |
|---|---|
| 5. 재귀 호출 - 완전 탐색, 동적 프로그래밍 (0) | 2020.07.31 |
| 4. 비트 조작 - 비트 연산자, 비트 함수 (0) | 2020.07.31 |
| 3. 자료구조 (3) - 힙, 구조체 (0) | 2020.07.25 |
| 1. 자료구조 (1) - 배열, 연결리스트, 스택, 큐 (0) | 2020.07.14 |

Comment